Planning in representation space

Agents parameterized by neural nets (Atari players etc.) seem to universally suffer from an ability to plan. This is obvious in the case of Markov reflex agents like vanilla deep Q learners, and seems to be true even of agents with some amount of hidden state (like the MemN2N paper at NIPS). Nevertheless planning-like behaviors have been successfully applied to other deep models, most notably text generation—beam decoding, and even beam-aware training, seem to be essential for both MT and captioning. And of course, real planning is ubiquitous among people working on non-toy control problems.

Task and motion planning is a good example. At the end of the day, we need to solve a continuous control problem, but attempting to solve this directly (either with a generic control policy or TrajOpt-like procedure) is too hard. Instead we come up with some highly simplified, hand-specified encoding of the problem—perhaps a STRIPS representation that discards geometry. We solve the (comparatively easy) STRIPS planning problem, and then project back down into motion planning space. This projection might not correspond to a feasible policy! (But we want things feasible in task space to be feasible in motion space as much as possible.) We keep searching in planning space until we find a solution that also works in task space.

This is really just a coarse-to-fine pruning scheme—we want a cheap way to discard plans that are obviously infeasible, so we can devote all of our computational resources to cases that really require simulation.

We can represent this schematically:

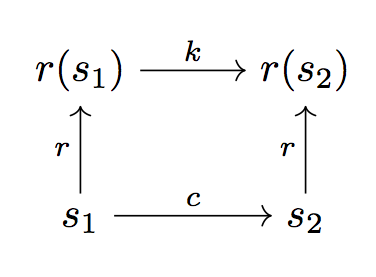
Here we have a representation function $r$ , a true cost function $c$ (which we may want to think of as a 0–1 feasibility judgment), and a “representation cost” $k$ . We want to ensure that $r$ is “close to an isomorphism” from motion costs to task costs, in the sense that $c(s_1, s_2) \approx k(r(s_1), r(s_2))$ .

For the STRIPS version, we assume that $r$ and $k$ are given to us by hand. But can we learn a better representation than STRIPS for solving task and motion planning problems?

Learning from example plans

First suppose that we have training data in the form of successful sequences with motion-space waypoints $(s_1, s_2, \ldots, s^*)$ . Then we can directly minimize an objective of the form

$L(\theta) = \sum_i \left[c(s_i, s_{i+1}) - k_\theta(r_\theta(s_i), r_\theta(s_{i+1}))\right]^2$

for $r$ and $k$ parameterized by $\theta$ . Easiest if representation space (the codomain of $r$ ) is $\mathbb{R}^d$ ; then we can manipulate $d$ to control the tradeoff between representation quality and the cost of searching in representation space.

Problem: if we only ever observe constant $c$ (which might be the case if we only see good solutions), there’s no pressure to learn a nontrivial $k$ . So we also want examples of unsuccessful attempts.

Decoding

Given a trained model, we can solve new instances by:

Sample a cost-weighted path through representation space $(r_1, r_2, ..., r_n)$ such that $r(s^*) \approx r_n$ .
Map each representation space transition $r_1 \to r_2$ onto a motion space transition $s_1 \to s_2$ such that $r(s_2) \approx r_2$ . (Easily expressed as an opt problem if $r$ is differentiable, but harder as a policy.)
Repeat until one of the motion-space solutions is feasible.

At every step that involves computing a path (whether in $r$ -space or $s$ -space, we can use a wide range of possible techniques, whether optimization-based (TrajOpt), search-based (RRT, though probably not in high dimensions), or by learning a policy parameterized by the goal state.

Learning directly from task feedback

What if we don’t have good traces to learn from? Just interleave the above two steps—starting from random initialization, roll out to a sequence of predicted $r$ and $s$ , then treat this as supervision, and again update $k$ to reflect observed costs.

Informed search

So far we’re assuming we can just brute-force our way through representation space until we get close to the goal. There’s nothing to enforce that closeness in representation space corresponds to closeness in motion space (other than the possible smoothness of $r$ ). We might want to add an additional constraint that if $r_i$ is definitely three hops from $r_n$ , then $||r_i - r_n|| > ||r_{i+1} - r_n||$ or something similar. This immediately provides a useful heuristic for the search in representation space.

We can also use side-information at this stage—maybe advice provided in the form of language or a video demonstration. (Then we need to learn another mapping from advice space to representation space.)

Modularity

It’s common to define several different primitive operations in the STRIPS domain—e.g. just “move” and “grasp”. We might analogously want to give our agent access to a discrete inventory of different policies, with associated transition costs $k_1, k_2, \ldots$ . Now the search problem involves both (continuously) choosing a set of points, and (discretely) choosing cost functions / motion primitives for moving between them. The associated motions of each of these primitives might be confined to some (hand-picked) sub-manifold of configuration space (e.g. only move the end effector, only move the first joint).

Thanks to Dylan Hadfield-Menell for useful discussions about task and motion planning.