A neural network is a monference, not a model
The distinction between models and inference procedures is central to most introductory presentations of artificial intelligence. For example: HMMs are a class of model; the Viterbi algorithm is one associated inference procedure, the forward–backward algorithm is another, and particle filtering is a third.
Many people describe (and presumably think of) neural networks as a class of models. I want to argue that this view is misleading, and that it is more useful to think of neural networks as hopelessly entangled model–inference pairs. “Model–inference pair” is a mouthful, and there doesn’t seem to be good existing shorthand, so I will henceforth refer to such objects as “monferences”. My claim is that we should think of a neural network as an example of a monference. (An implementation of the Viterbi algorithm, equipped with the parameters of some fixed HMM, is also a monference.)
I’m about to cite a bunch of existing papers that follow naturally from the neural-nets-as-monferences perspective—it seems like this idea is already obvious to a lot of people. But I don’t think it’s been given a name or a systematic treatment, and I hope others will find what follows as useful (or at least as deconfounding) as I did.
What are the consequences of regarding a neural net as a model? A personal example is illustrative:
The first time I saw a recurrent neural network, I thought “this is an interesting model with a broken inference procedure”. A recurrent net looks like an HMM. An HMM has a discrete hidden state, and a recurrent net has a vector-valued hidden state. When we do inference in an HMM, we maintain a distribution over hidden states consistent with the output, but when we do inference in a recurrent net, we maintain only a single vector—a single hypothesis, and a greedy inference procedure. Surely things would be better if there were some way of modeling uncertainty? Why not treat RNN inference like Kalman filtering?
This complaint is wrong. Our goal in the remainder of this post is to explore why it’s wrong.
Put simply, there is no reason to regard the hidden state of a recurrent network as a single hypothesis. After all, a sufficiently large hidden vector can easily represent the whole table of probabilities we use in the forward algorithm—or even represent the state of a particle filter. The analogy “HMM hidden state = RNN hidden state” is bad; a better analogy is “HMM decoder state = RNN hidden state”.
Let’s look at this experimentally. (Code for this section can be found in the accompanying Jupyter notebook.)
If we think about the classical inference procedure with the same structure as a (uni-directional) recurrent neural network, it’s something like this: for , receive an emission from the HMM, and immediately predict a hidden state . You should be able to convince yourself that if we’re evaluated on tagging accuracy, the min-risk monference (if HMM parameters are known) is to run the forward algorithm, and predict the tag with maximum marginal probability at each time .
I generated a random HMM, drew a bunch of sequences from it, and applied this min-risk classical procedure. I obtained the following “online tagging” accuracy:
62.8Another totally acceptable (though somewhat more labor-intensive) way of producing a monference for this online tagging problem is to take the HMM, draw many more samples from it, and use the (observed, hidden) sequences as training data (x, y) for a vanilla RNN of the following form:
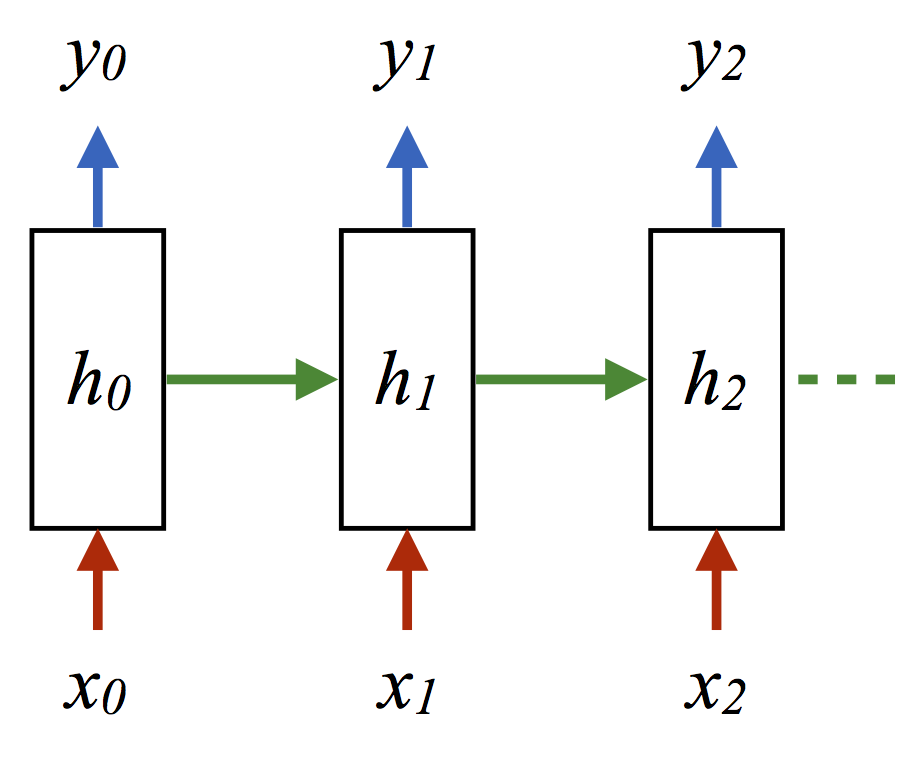
(where each arrow is an inner product followed by a ReLU or log-loss). In this case I obtained the following accuracy:
62.8Is it just a coincidence that these scores are the same? Let’s look at some predictions:
true hidden sequence: 1 0 0 1 0
classical monference: 1 0 1 1 0
neural monference: 1 0 1 1 0
true hidden sequence: 1 0 1 2 0
classical monference: 1 0 1 0 0
neural monference: 1 0 1 0 0So even when our two monferences are wrong, they’re wrong in the same way.
Of course, we know that we can get slightly better results for this problem by running the full forward-backward algorithm, and again making max-marginal predictions. This improved classical procedure gave an accuracy of:
63.3better than either of the online models, as expected. Training a bidirectional recurrent net
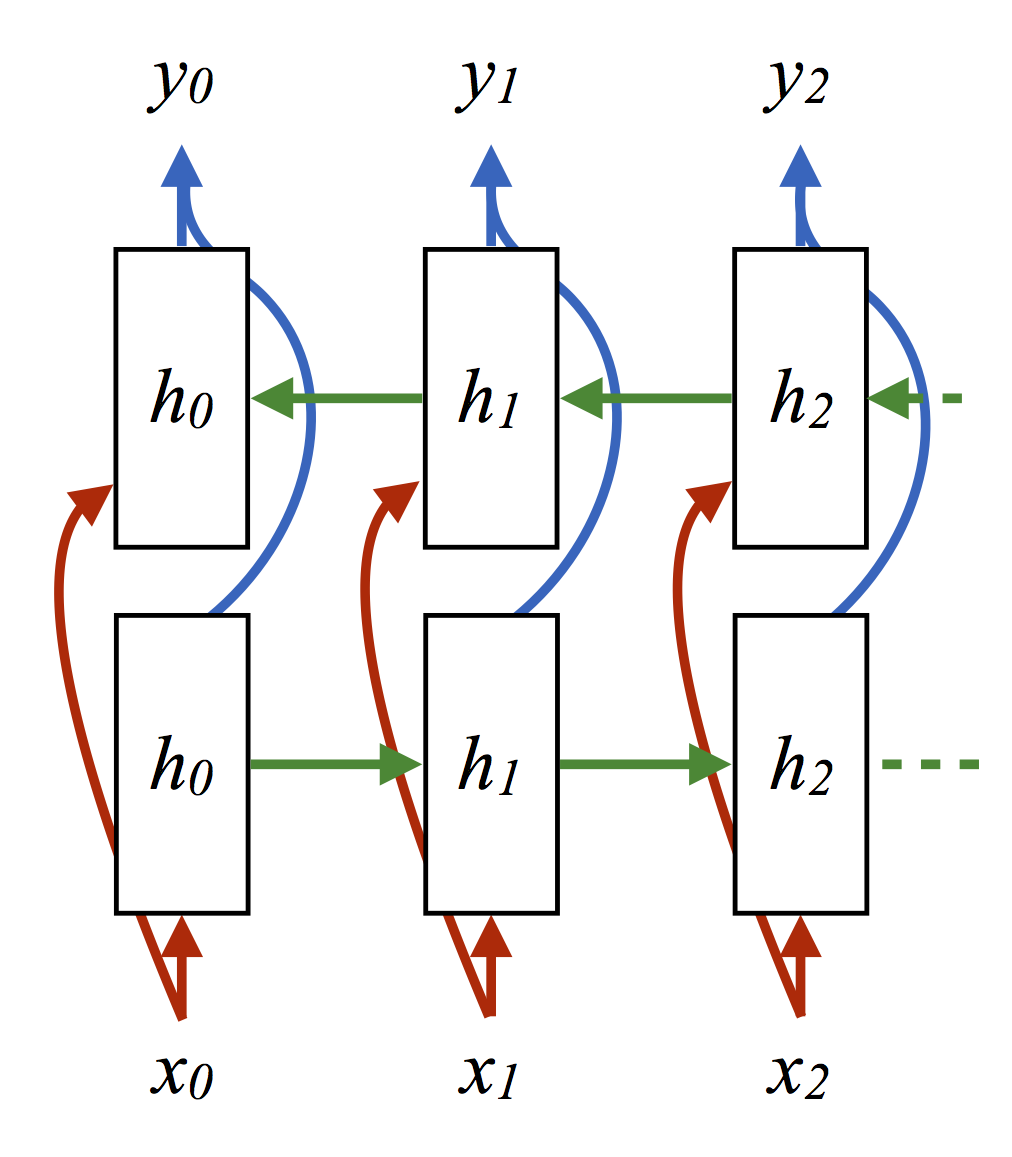
on samples from the HMM gave a tagging accuracy of:
63.3A sample prediction:
true hidden sequence: 0 1 0 0 1
classical monference: 0 1 0 0 1
neural monference: 0 1 0 0 1Notice: the neural nets we’ve used here don’t encode anything about classical message-passing rules, and they definitely don’t encode anything about the generative process underlying an HMM. Yet in both cases, the neural net managed to achieve accuracy as good as (but no better than) the classical message passing procedure with the same structure. Indeed, this neural training procedure results in a piece of code that makes identical predictions to the forward–backward algorithm, but it doesn’t know anything about the forward–backward algorithm!
Neural networks are not magic—when our data is actually generated from an HMM, we can’t hope to beat an (information-theoretically optimal) classical monference with a neural one. But we can empirically do just as well. As we augment neural architectures to match the algorithmic structure of more powerful classical inference procedures, their performance improves. Bidirectional recurrent nets are better than forward-only ones; bidirectional networks with multiple layers between each “real” hidden vector might be even better for some tasks.
Better yet, we can perhaps worry less about harder cases, when we previously would have needed to hand-tune some approximate inference scheme. (One example: suppose our transition matrix is a huge permutation. It might be very expensive to do repeated multiplications for classical inference, and trying to take a low-rank approximation to the transition matrix will lose information. But a neural monference can potentially represent our model dynamics quite compactly.)
So far we’ve been looking at sequences, but analogues for more structured data exist as well. For tree-shaped problems, we can run something that looks like the inside algorithm over a fixed tree or the inside–outside algorithm over a whole sparsified parse chart. For arbitrary graphs, we can apply repeated “graph convolutions” that start to look a lot like belief propagation.
There’s a general principle here: anywhere you have an inference algorithm that maintains a distribution over discrete states, instead:
- replace {chart cells, discrete distributions} with vectors
- replace messages between cells with recurrent networks
- unroll the “inference” procedure for a suitable number of iterations
- train via backpropagation
The resulting monference has at least as much capacity as the corresponding classical procedure. To the extent that appproximation is necessary, we can (at least empirically) learn the right approximation end-to-end from the training data.
(The version of this that backpropagates through an approximate inference procedure, but doesn’t attempt to learn the inference function itself, has been around for a while.)
I think there’s at least one more constituency parsing paper to be written using all the pieces of this framework, and lots more for working with graph-structured data.
I’ve argued that the monference perspective is useful, but is it true? That is, is there a precise sense in which a neural net is really a monference, and not a model?
No. There’s a fundamental identifiability problem—we can’t really distinguish between “fancy model with trivial inference” and “mystery model with complicated inference”. Thus it also makes no sense to ask, given a trained neural network, which model it performs inference for. (On the other hand, networks trained via distillation seem like good candidates for “same model, different monference”.) And the networks-as-_models_ perspective shouldn’t be completely ignored: it’s resulted in a fruitful line of work that replaces log-linear potentials with neural networks inside CRFs. (Though one of the usual selling points of these methods is that “you get to keep your dynamic program”, which we’ve argued here is true of suitably organized recurrent networks as well.)
In spite of all this, as research focus in this corner of the machine learning community shifts towards planning, reasoning, and harder algorithmic problems, I think the neural-nets-as-monferences perspective should dominate.
More than that—when we look back on the “deep learning revolution” ten years from now, I think the real lesson will be the importance of end-to-end training of decoders and reasoning procedures, even in systems that barely look like neural networks at all. So when building learning systems, don’t ask: “what is the probabilistic relationship among my variables?”. Instead ask: “how do I approximate the inference function for my problem?”, and attempt to learn this approximation directly. To do this effectively, we can use everything we know about classical inference procedures. But we should also start thinking of inference as a first-class part of the learning problem.
Thanks to Matt Gormley (whose EMNLP talk got me thinking about these issues), and Robert Nishihara and Greg Durrett for feedback.
Also Jason Eisner for this gem: “An awful portmanteau, since monference should be a count noun like model, but you took the suffix from the mass noun. Not that I can claim that infedel is much better…”